Fast, Streaming AJAX proxy – continuously download from cross domain

Due to browser’s prohibition on cross
domain XMLHTTP call, all AJAX websites must have server side proxy
to fetch content from external domain like Flickr or Digg. From
client side javascript code, an XMLHTTP call goes to the server
side proxy hosted on the same domain and then the proxy downloads
the content from the external server and sends back to the browser.
In general, all AJAX websites on the Internet that are showing
content from external domains are following this proxy approach
except some rare ones who are using JSONP. Such a proxy gets a very
large number of hits when a lot of component on the website are
downloading content from external domains. So, it becomes a
scalability issue when the proxy starts getting millions of hits.
Moreover, web page’s overall load performance largely depends on
the performance of the proxy as it delivers content to the page. In
this article, we will take a look how we can take a conventional
AJAX Proxy and make it faster, asynchronous, continuously stream
content and thus make it more scalable.

You can see such a proxy in action when you go to Pageflakes.com. You will see
flakes (widgets) loading many different content like weather feed,
flickr photo, youtube videos, RSS from many different external
domains. All these are done via a Content Proxy. Content
Proxy served about 42.3 million URLs last month which is
quite an engineering challenge for us to make it both fast and
scalable. Sometimes Content Proxy serves megabytes of data, which
poses even greater engineering challenge. As such proxy gets large
number of hits, if we can save on an average 100ms from each call,
we can save 4.23 million seconds of
download/upload/processing time every month. That’s about 1175 man
hours wasted throughout the world by millions of people staring at
browser waiting for content to download.

Such a content proxy takes an external server’s URL as a query
parameter. It downloads the content from the URL and then writes
the content as response back to browser.

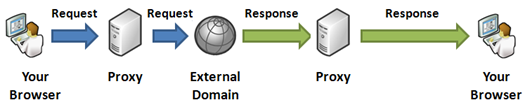
Figure: Content Proxy working as a middleman between browser and
external domain

The above timeline shows how request goes to the server and then
server makes a request to external server, downloads the response
and then transmits back to the browser. The response arrow from
proxy to browser is larger than the response arrow from external
server to proxy because generally proxy server’s hosting
environment has better download speed than the user’s Internet
connectivity.

Such a content proxy is also available in my open source Ajax
Web Portal Dropthings.com.
You can see from its
code how such a proxy is implemented.

The following is a very simple synchronous, non-streaming,
blocking Proxy:

[WebMethod]
[ScriptMethod(UseHttpGet=true)]
public string GetString(string url)
{
        using (WebClient client = new WebClient())
        {
            string response = client.DownloadString(url);
            return response;
        }
    }
}

Although it shows the general principle, but it’s no where close
to a real proxy because:

• It’s a synchronous proxy and thus not scalable. Every call to
  this web method causes the ASP.NET thread to wait until the call to
  the external URL completes.
• It’s non streaming. It first downloads the entire
  content on the server, storing it in a string and then uploading
  that entire content to the browser. If you pass MSDN feed URL, it will
  download that gigantic 220 KB RSS XML on the server and store it on
  a 220 KB long string (actually double the size as .NET strings are
  all Unicode string) and then write 220 KB to ASP.NET Response
  buffer, consuming another 220 KB UTF8 byte array in memory. Then
  that 220 KB will be passed to IIS in chunks so that it can transmit
  it to the browser.
• It does not produce proper response header to cache the
  response on the server. Nor does it deliver important headers like
  Content-Type from the source.
• If external URL is providing gzipped content, it decompresses
  the content into a string representation and thus wastes server
  memory.
• It does not cache the content on the server. So, repeated call
  to the same external URL within the same second or minute will
  download content from the external URL and thus waste bandwidth on
  your server.

So, we need an asynchronous streaming proxy that
transmits the content to the browser while it downloads from the
external domain server. So, it will download bytes from external
URL in small chunks and immediately transmit that to the browser.
As a result, browser will see a continuous transmission of bytes
right after calling the web service. There will be no delay while
the content is fully downloaded on the server.

Before I show you the complex streaming proxy code, let’s take
an evolutionary approach. Let’s build a better Content Proxy that
the one shown above, which is synchronous, non-streaming but does
not have the other problems mentioned above. We will build a HTTP
Handler named RegularProxy.ashx which will take url
as a query parameter. It will also take cache as a query
parameter which it will use to produce proper response headers in
order to cache the content on the browser. Thus it will save
browser from downloading the same content again and again.

<%@ WebHandler Language="C#" Class="RegularProxy" %>

using System;
using System.Web;
using System.Web.Caching;
using System.Net;
using ProxyHelpers;
public class RegularProxy : IHttpHandler {
        
    public void ProcessRequest (HttpContext context) {
        string url = context.Request["url"];
        int cacheDuration = Convert.ToInt32(context.Request["cache"]?? "0");
        string contentType = context.Request["type"];

        // We don't want to buffer because we want to save memory
        context.Response.Buffer = false;
            
        // Serve from cache if available
        if (context.Cache[url] != null)
        {
            context.Response.BinaryWrite(context.Cache[url] as byte[]);
            context.Response.Flush();
            return;
        }
        using (WebClient client = new WebClient())
        {
            if (!string.IsNullOrEmpty(contentType))
                client.Headers["Content-Type"] = contentType;
            
            client.Headers["Accept-Encoding"] = "gzip";
            client.Headers["Accept"] = "*/*";
            client.Headers["Accept-Language"] = "en-US";
            client.Headers["User-Agent"] = 
"Mozilla/5.0 (Windows; U; Windows NT 6.0; en-US; rv:1.8.1.6) Gecko/20070725 Firefox/2.0.0.6";
            
            byte[] data = client.DownloadData(url);

            context.Cache.Insert(url, data, null,
                        Cache.NoAbsoluteExpiration,
                        TimeSpan.FromMinutes(cacheDuration),
                        CacheItemPriority.Normal, null); 
            
            if (!context.Response.IsClientConnected) return;

            
            // Deliver content type, encoding and length as it is received from the external URL
            context.Response.ContentType = client.ResponseHeaders["Content-Type"];
            string contentEncoding = client.ResponseHeaders["Content-Encoding"];
            string contentLength = client.ResponseHeaders["Content-Length"];

            if (!string.IsNullOrEmpty(contentEncoding))
                context.Response.AppendHeader("Content-Encoding", contentEncoding);
            if (!string.IsNullOrEmpty(contentLength))
                context.Response.AppendHeader("Content-Length", contentLength);

            if (cacheDuration > 0)
                HttpHelper.CacheResponse(context, cacheDuration);
            
            // Transmit the exact bytes downloaded
            context.Response.BinaryWrite(data);
        }
    }
 
    public bool IsReusable {
        get {
            return false;
        }
    }

}

There are two enhancements in this proxy:

• It allows server side caching of content. Same URL requested by
  a different browser within a time period will not be downloaded on
  server again, instead it will be served from cache.
• It generates proper response cache header so that the content
  can be cached on browser.
• It does not decompress the downloaded content in memory. It
  keeps the original byte stream intact. This saves memory
  allocation.
• It transmits the data in non-buffered fashion, which means
  ASP.NET Response object does not buffer the response and thus saves
  memory

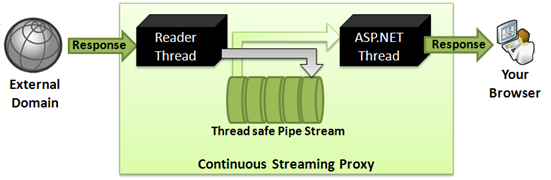
However, this is a blocking proxy. We need to make a streaming
asynchronous proxy for better performance. Here’s why:

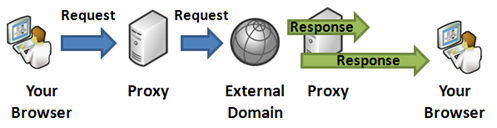
Figure: Continuous streaming proxy

As you see, when data is transmitted from server to browser
while server downloads the content, the delay for server side
download is eliminated. So, if server takes 300ms to download
something from external source, and then 700ms to send it back to
browser, you can save up to 300ms Network Latency between server
and browser. The situation gets even better when the external
server that serves the content is slow and takes quite some time to
deliver the content. The slower external site is, the more saving
you get in this continuous streaming approach. This is
significantly faster than blocking approach when the external
server is in Asia or Australia and your server is in USA.

The approach for continuous proxy is:

• Read bytes from external server in chunks of 8KB from a
  separate thread (Reader thread) so that it’s not blocked
• Store the chunks in an in-memory Queue
• Write the chunks to ASP.NET Response from that same queue
• If the queue is finished, wait until more bytes are downloaded
  by the reader thread

The Pipe Stream needs to be thread safe and it needs to support
blocking Read. By blocking read it means, if a thread tries to read
a chunk from it and the stream is empty, it will suspend that
thread until another thread writes something on the stream. Once a
write happens, it will resume the reader thread and allow it to
read. I have taken the code of PipeStream from CodeProject
article by James Kolpack and extended it to make sure it’s high
performance, supports chunks of bytes to be stored instead of
single bytes, support timeout on waits and so on.

A did some comparison between Regular proxy (blocking,
synchronous, download all then deliver) and Streaming Proxy
(continuous transmission from external server to browser). Both
proxy downloads the MSDN feed and delivers it to the browser. The
time taken here shows the total duration of browser making the
request to the proxy and then getting the entire response.

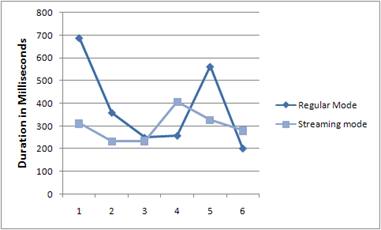
Figure: Time taken by Streaming Proxy vs Regular Proxy while
downloading MSDN feed

Not a very scientific graph and response time varies on the link
speed between the browser and the proxy server and then from proxy
server to the external server. But it shows that most of the time,
Streaming Proxy outperformed Regular proxy.

Figure: Test client to compare between Regular Proxy and Streaming
Proxy

You can also test both proxy’s response time by going to
http://labs.dropthings.com/AjaxStreamingProxy.
Put your URL and hit Regular/Stream button and see the “Statistics”
text box for the total duration. You can turn on “Cache response”
and hit a URL from one browser. Then go to another browser and hit
the URL to see the response coming from server cache directly. Also
if you hit the URL again on the same browser, you will see response
comes instantly without ever making call to the server. That’s
browser cache at work.

Learn more about Http Response caching from my blog post:

Making best use of cache for high performance website

A Visual Studio Web Test run inside a Load Test shows a better
picture:

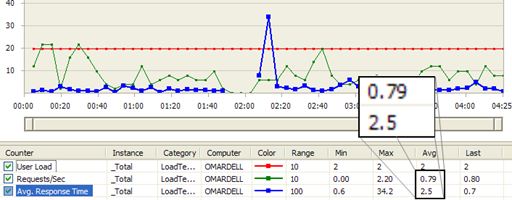
Figure: Regular Proxy load test result shows Average
Requests/Sec 0.79 and Avg Response Time 2.5 sec

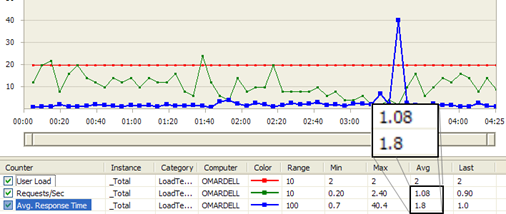
Figure: Streaming Proxy load test result shows Avg Req/Sec is
1.08 and Avg Response Time 1.8 sec.

From the above load test results, Streaming Proxy is 26%
better Request/Sec and Average Response Time is 29% better. The
numbers may sound small, but at Pageflakes, 29% better response
time means 1.29 million seconds saved per month for all the
users on the website. So, we are effectively saving 353 man hours
per month which was wasted staring at browser screen while it
downloads content.

Building the Streaming Proxy

The details how the Streaming Proxy is built is quite long and
not suitable for a blog post. So, I have written a CodeProject
article:

Fast, Scalable,
Streaming AJAX Proxy – continuously deliver data from cross
domain

Please read the article and please vote for me if your find it
useful.